The game "kreski" is finite

The proof is based on an observation that during each game the difference between the number of points and the number of lines is 36. At the beginning of the game there are 36 points and no lines. At each move one line and one point are added, so the difference is constant.

Let us consider a rectangular grid of points (i,j) where i and j are integer numbers. An interval with the endpoints (i,j) and (k,l) where max(|k-i|,|l-j|)=1 is called a unit line. An interval with the endpoints (i,j) and (k,l) where max(|k-i|,|l-j|)=4 is called a line of the length 4 or a line for short.

Each initial point can be used to draw lines in 8 directions. Therefore at the beginning of a game we have 36*8=288 unused directions. At each move we use 6 or 7 directions from existing points and create a new point with 6 or 7 unused directions (depending on whether the new point is the end of the added line or not). The number of unused directions is not changed. The game must end because any set of grid points on the plane has a border and at a border some directions are not used (are lost).

An upper bound is found be considering convex sets of grid points with the number L of directions lost at the border not larger than 288 and counting the number of unit lines withing this set. If we have a set which is not convex then it might be enlarged to a convex set with the same or smaller number of directions lost at the border. It is clear that the only convex sets of grid points with borders composed of unit lines are octagons (or degenerate octagons where some edges have zero length). Let us consider an octagon with sides of length n₁,n₂,n₃,n₄,n₅,n₆,n₇,n₈ (in the maximum metric), where n₁,n₂,...,n₈ are non-negative. If all these numbers are positive we obtain a proper octagon, otherwise the octagon is degenerate (it is a polygon with the number of sides less than 8). We assume that the first side goes up, the second one goes up-right, the third one goes to the right and so on. The following conditions must be satisfied: n₈+n₁+n₂=n₄+n₅+6 and n₂+n₃+n₄=n₈+n₇+n₆. We assume that the octagon is enclosed in the region x>=0 and y>=0 and has non-empty intersections with the axes x=0 and y=0. The vertices of this octagon are (0,n₈),(0,n₈+n₁),(n₂,n₈+n₁+n₂),(n₂+n₃,n₈+n₁+n₂),(n₂+n₃+n₄,n₈+n₁+n₂-n₄),(n₂+n₃+n₄,n₈+n₁+n₂-n₄-n₅),(n₂+n₃+n₄-n₆,n₈+n₁+n₂-n₄-n₅-n₆)=(n₈+n₇,0),(n₂+n₃+n₄-n₆-n₇,n₈+n₁+n₂-n₄-n₅-n₆)=(n₈,0). We are interested in octagons for which the number of lost directions at the border is not larger that 36*4=288. The number of lost directions for this octagon can be computed as L=3*(n₁+n₃+n₅+n₇)+4*(n₂+n₄+n₆+n₈)+8.

Below, three bounds for the maximum number M of moves is given.

M≤705

One may show that octagons with L≤288 cannot contain more than 2820 unit lines (unit lines at the border are also counted). The maximum is realized for n₁=n₂=n₃=n₄=n₅=n₆=n₇=n₈=10. The octagon coordinates are (0,10),(0,20),(10,30),(20,30),(30,20),(30,10),(20,10),(10,0). With 2820 unit lines the maximum number of lines of the length 4 cannot be larger than 2820/4=705. The C++ code with the algorithm verifying this statement can be found here .

M≤673

A slightly better bound can be found by counting the maximum number of horizontal, vertical and diagonal lines which may by drawn in such polygons. One may show that the maximum number of vertical and horizontal lines is not larger than 343. The maximum is obtained for n₁=12, n₂=10,n₃=8, n₄=10, n₅=12, n₆=10, n₇=8, n₈=10. One may also show that the maximum number of diagonal lines cannot be larger that 330. The maximum is obtained for the octagon with n₁=13, n₂=8, n₃=12, n₄=9, n₅=11, n₆=9, n₇=12, n₈=8. This gives the bound 343+330=673.

M≤665

An even better bound can be obtained by finding a polygon with the maximum number of vertical, horizontal and diagonal lines. The maximum of 665 lines is obtained for the same octagon as for the diagonal lines, i.e., n₁=13, n₂=8, n₃=12, n₄=9, n₅=11, n₆=9, n₇=12, n₈=8. The octagon with 665 vertical, horizontal and diagonal lines is shown below
665

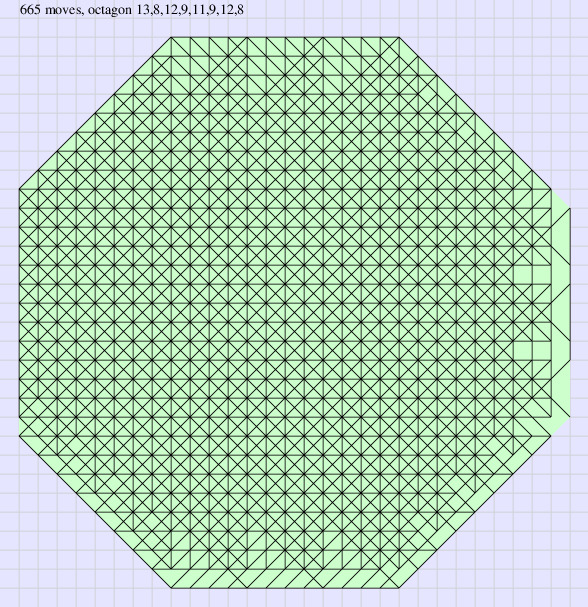
Clearly the bound 665 is a huge overestimation as many directions are necessarily lost inside octagons. The best solution of the 5T++ problem found by Boyer contains 317 lines (www.morpionsolitaire.com). This is perhaps a true bound for the problem of finding a set of points with the maximum number of lines and the number of lost directions equal to 288.